[technology][機械学習][scikit-learn]python3 + scikit-learnで時系列データの異常検知を実験
概要
時系列データ(複数ではなく、単純に時間軸に沿って、1種類のデータが並んでいるもの、例えばNICの通信量だったり、CPUの動作率だったり)から異常な動きを検出するいわゆる異常値検出を調べていたのですが、種々手法がある中で、「クラスタリングを使う」「スライディングウィンドウで時系列データを切り出し、個々のウィンドウの中のデータをベクトル化」みたいな流れは判ったのですが、とりあえず外れ値検知とおぼしきコードをscikit-learnのKMeansで組んでみました。
環境
Ubuntu16.04LTS+Anaconda3(python3.6)
やったこと
ソースを細かく説明したいのですが、とりあえずざっくりと。
- 0〜359度までのSIN関数の値を360点の時系列データとして生成
- 適当に異常値を入れるポイントを選び、本来のSINの値の1/2に置き換える
- 出来上がった時系列データの階差データを取る(359点の階差データが出来る)
- ウィンドウサイズを適当に決める(下記ソースでは4)
- ウィンドウサイズに合わせて、階差データを4点づつベクトル化する
階差データがd0,d1,d2,d3,d4,d5,d6,,.....とするとベクトル化したデータは(d0,d1,d2,d3),(d1,d2,d3,d4),(d2,d3,d4,d5)...という感じでベクトルの要素が1個づつ後ろにずれて入る
ソース
# -*- Coding: utf-8 -*-
# numpy
import numpy as np
# scikit-learnx
from sklearn.cluster import KMeans
# Matplotlib
import matplotlib as mpl
mpl.use('TkAgg') # or whatever other backend that you want
import matplotlib.pyplot as plt
from matplotlib import cm
# Windows Size
WSZ = 4
# 異常値を生成する角度のリスト
a_angles = [60,90,120,270,320]
# SINカーブを作る(0〜359度)
x = np.arange(0,360)
y = np.sin(x * np.pi/180)
# 異常値を作る
for angle in a_angles:
y[angle] = y[angle] * 0.5
# 階差行列を作る
yd = np.diff(y)
# 階差行列にスライディングウィンドウを適用してベクトル化
ydlist = []
for i in range(0,359 - WSZ):
ydlist.append(yd[i:i+WSZ])
ydlist = np.array(ydlist)
# スライディングウィンドウでベクトル化した階差データ列をKMeansでクラスタリング
kmeans = KMeans(n_clusters=8)
kmeans_model = kmeans.fit(ydlist)
# 各スライディングウィンドウのラベル(グループ番号)リストを取得
labels = kmeans_model.labels_
# 時系列データ(SIN波+異常データ)とクラスタリング結果を並べてグラフを描く
nlabels = np.r_[np.zeros(1,dtype=np.int32),labels,np.zeros(WSZ,dtype=np.int32)]
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
ax1.plot(x,y,label='wave form')
ax2.plot(x,nlabels,label='check result')
ax1.legend()
ax2.legend()
plt.show()
結果を描画したグラフ
正常なところがグループ0,異常値を含むウィンドウが0以外のグループ番号になっているのが判ると思います。
もっと複雑なデータで実行する場合は、ウィンドウサイズの調整等が必要になると思います。
グラフ上、異常値の場所より少し前に非0のグループ番号がある様に見えるのは、グループ番号の表示位置を各ウィンドウの先頭の階差データの位置に合わせたからです。
(異常値がそのウィンドウの最後に現れる。グループ番号はそのウィンドウの先頭のプロットされている。)
次は同じ手法で作った階差ベクトルをJubatusのアノマリ検知に食わせてみようかと思っています。
追記: 参考にしたのは下記のブログです
が、コードが理解しきれなかったので、自分で簡単な波形で考えながら書いたのが上記のコードです。
非常に異常値が分かりやすい例なので、もっと複雑な波形で上手く行くかは判りません。
blog.brains-tech.co.jp
追記2:
階差ベクトルのクラスタリングというのが何をやっているのか判りやすい様に可視化してみました。
# Windows Size WSZ = 2
上記のソースで階差ベクトルを作るためのウィンドウサイズを2に変更します。
こうすると各階差ベクトルは2次元のベクトルになります。
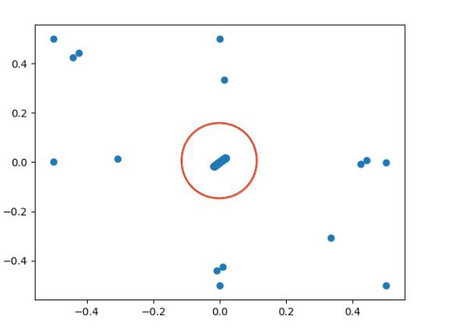
plt.scatter(ydlist[:,0],ydlist[:,1]) plt.show()
2次元のベクトルなので、そのままmatplotlibでプロットしてみます。
その結果が下記です。正常なSIN波の階差ベクトルが原点付近に固まっているのが判ります。(赤丸の中)
そして通常の値の変動率(要は微分値)から大きく外れたベクトルが原点から離れた位置にあるのが判ります。
複雑な波形の場合は、これを3,4,5次元と...どんどん次元拡張していけば、考え方は同じになります。